En esta clase realizaremos la implementación de un modelo de red neuronal para predicción de un valor continuo. Para ello trabajaremos con el conjunto de datos iris:
import seaborn as sns
print('Conjuntos de datos disponibles en seaborn: ')
for _ in sns.get_dataset_names():
print(_, end=', ')
Conjuntos de datos disponibles en seaborn: anagrams, anscombe, attention, brain_networks, car_crashes, diamonds, dots, dowjones, exercise, flights, fmri, geyser, glue, healthexp, iris, mpg, penguins, planets, seaice, taxis, tips, titanic,
# cargamos el conjunto de datos iris
df = sns.load_dataset('iris')
df.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
Y consideraremos un dataframe con las correlaciones ntre dichas variables
df.corr(method='pearson')
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| sepal_length | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| sepal_width | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| petal_length | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| petal_width | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
Notamos que petal_width con petal_length están altamente correlacionadas. Gráficamente
ax = df.plot.scatter(x='petal_width', y='petal_length', c='blue', grid=True)
Para la primera parte de esta clase trabajaremos únicamente con las dos variables anteriores
# seleccionamos solo las dos variables de interes
df_reducido = df[['petal_width', 'petal_length']]
Lo que haremos inicialmente será implementar un modelo de regresión lineal simple, donde petal_width será la variable regresora y petal_length será la variable de respuesta. Después de ajustar el modelo de regresión con los datos de entrenamiento, realizaremos predicciones sobre el conjunto de prueba. Para ello
# Importacion necesaria
from sklearn.model_selection import train_test_split
# definimos las variables
X = df['petal_width'].values.reshape(-1,1)
y = df['petal_length'].values.reshape(-1,1)
# division de los datos
X_train, X_test, y_train, y_test = train_test_split(X, y, # conjunto completo
test_size=0.25, # 25% para pruebas
random_state=123) # semilla aleatoria
Procedemos a realizar el modelo de regresión y el ajuste
from sklearn.linear_model import LinearRegression
# instanciamos
reg = LinearRegression()
# ajustamos sobre los datos de entrenamiento
reg.fit(X_train, y_train)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
LinearRegression()
Realizamos ahora la predicción sobre el conjunto de pruebas y comparamos resultados mediante un dataframe
# predicion
y_pred_regression = reg.predict(X_test)
# dataframe con la informacion
df_info = pd.DataFrame(y_pred_regression).rename(columns = {0: 'y_pred_reg'})
df_info['y_test'] = y_test
df_info = df_info.reset_index()
# calculamos las diferencias entre los valores reales y los predichos
df_info['diff'] = abs(df_info.y_pred_reg - df_info.y_test)
# calculamos el porcentaje de error para cada fila
df_info['error'] = (df_info['diff'] * 100) / df_info['y_test']
df_info.head()
| index | y_pred_reg | y_test | diff | error | |
|---|---|---|---|---|---|
| 0 | 0 | 4.409119 | 4.9 | 0.490881 | 10.017988 |
| 1 | 1 | 5.736517 | 5.5 | 0.236517 | 4.300308 |
| 2 | 2 | 5.957750 | 5.6 | 0.357750 | 6.388392 |
| 3 | 3 | 3.966653 | 4.1 | 0.133347 | 3.252378 |
| 4 | 4 | 1.311856 | 1.4 | 0.088144 | 6.296008 |
Veamos un dataframe con estadísticas sobre la información anterior
df_info.describe()
| index | y_pred_reg | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.489255 | 3.544737 | 0.356043 | 11.113797 |
| std | 11.113055 | 1.801369 | 1.911374 | 0.264684 | 6.819835 |
| min | 0.000000 | 1.311856 | 1.100000 | 0.002953 | 0.089495 |
| 25% | 9.250000 | 1.533089 | 1.425000 | 0.133154 | 6.319104 |
| 50% | 18.500000 | 3.856036 | 4.050000 | 0.274186 | 9.833552 |
| 75% | 27.750000 | 5.072818 | 5.075000 | 0.506806 | 14.613545 |
| max | 37.000000 | 6.178983 | 6.700000 | 1.078983 | 31.703670 |
Tenemos que el error porcentual (el referente a la columna error) fue en promedio del 11.11%; el error máximo fue del 31.7% y el mínimo del 0.08%. El 75% de los errores fue menor al 14.61% y el 50% de los errores fue menor al 9.83%. De tal manera, parece ser que el ajuste de la regresión sobre los datos fue muy bueno. Podemos comprobar dicho rendimiento mediante las siguientes métricas
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
# error cuadratico medio
mse = mean_squared_error(y_pred_regression, y_test)
# R^2
r2 = r2_score(y_pred_regression, y_test)
# veamos
print(f'mse = {mse}\nR^2 = {r2}')
mse = 0.19498031795213722 R^2 = 0.9382883033472239
tenemos que el mse es pequeño y la $R^{2}$ es cercana a 1, de donde tenemos que el modelo de regresión obtenido es muy bueno.
Podemos ver un gráfico para observar qué tan buenas fueron nuestras predicciones. Para ello realizaremos un gráfico de líneas como sigue:
plt.plot(df_info.index, df_info.y_pred_reg, color='blue', label='prediccioón')
plt.plot(df_info.index, df_info.y_test, color='red', label='real')
plt.legend()
plt.grid()
plt.show()
Podemos observar un ajuste muy bueno de la predicción a los valores reales.
Lo que haremos después será la implementación de una red neuronal para predecir los valores de la variable petal_length.
En esta ocasión utilizaremos sólo la función de activación ReLu:
$$ ReLu(x)=max(0, x) $$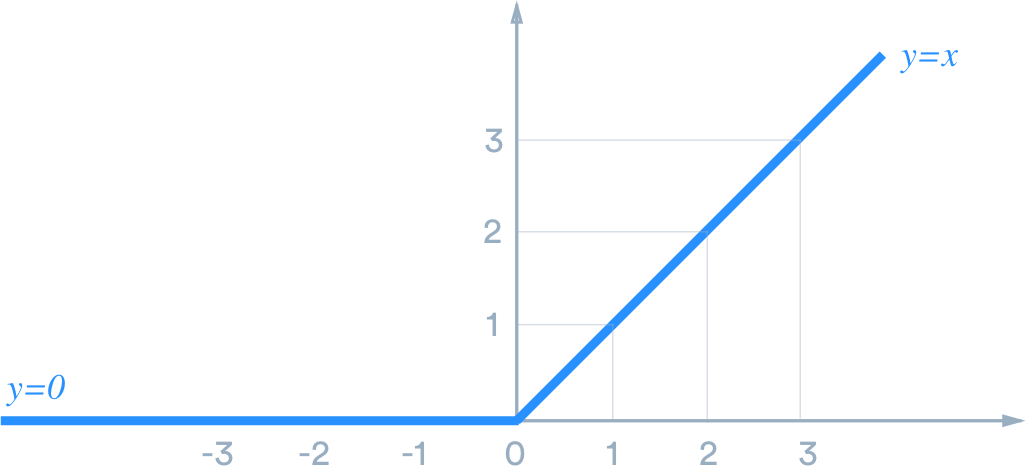
dado que querremos mantener los valores continuos que le vayamos pasando a la red. Por ejemplo, no sería conveniente utilizar la función de activación sigmoide debido a que ésta se utiliza para problemas de clasificación binaria.
Además, para problemas de predición de valores continuas, es común utilizar la función de pérdida del error cuadrático medio.
De tal manera, definimos la siguiente función:
from keras.models import Sequential
from keras.layers import Dense
def modelo(n1, n2, activacion, epocas, boolean):
"""
n1: número de neuronas en la primer capa
n2: número de neuronas en la segunda capa
activacion: función de activación en la última capa
epocas: número de épocas
boolean: booleano para determinar el valor de verbose
"""
# Instanciamos el modelo
model = Sequential()
# Capa de entrada de 1 neurona y capa oculta de n1 neuronas.
# Para la capa oculta utilizamos la funcion de activacion relu
model.add(Dense(n1, activation='relu', input_shape=(1,)))
# Capa oculta 2:
# n2 neuronas y funcion de activacion relu
model.add(Dense(n2, activation='relu'))
# Capa de salida con funcion de activacion "activacion"
model.add(Dense(1, activation=activacion))
# Compilacion. Utilizaremos ahora el error cuadratico medio
model.compile(optimizer='adam', loss='mean_squared_error')
# Entrenamiento
modelo = model.fit(X_train, y_train, epochs=epocas, verbose = boolean)
# prediccion
y_pred = model.predict(X_test)
# dataframe con la informacion
df = pd.DataFrame(y_pred).rename(columns = {0: 'y_pred'})
df['y_test'] = y_test
df = df.reset_index()
df['diff'] = abs(df.y_pred - df.y_test)
df['error'] = (df['diff'] * 100) / df['y_test']
# estadisticas
df_stats = df.describe()
# grafica
plt.plot(df.index, df.y_pred, color='blue', label='prediccioón')
plt.plot(df.index, df.y_test, color='red', label='real')
plt.legend()
plt.grid()
plt.show()
# MSE
mse = mean_squared_error(y_pred, y_test)
print(f'mse = {mse}')
return modelo, df, df_stats
Implementamos un primer modelo
modelo1, df1, df_stats1 = modelo(40, 25, 'relu', 13, True)
df_stats1
Epoch 1/13 4/4 [==============================] - 0s 2ms/step - loss: 16.4030 Epoch 2/13 4/4 [==============================] - 0s 2ms/step - loss: 15.8458 Epoch 3/13 4/4 [==============================] - 0s 2ms/step - loss: 15.3099 Epoch 4/13 4/4 [==============================] - 0s 3ms/step - loss: 14.7636 Epoch 5/13 4/4 [==============================] - 0s 2ms/step - loss: 14.2382 Epoch 6/13 4/4 [==============================] - 0s 2ms/step - loss: 13.6806 Epoch 7/13 4/4 [==============================] - 0s 2ms/step - loss: 13.0921 Epoch 8/13 4/4 [==============================] - 0s 2ms/step - loss: 12.4487 Epoch 9/13 4/4 [==============================] - 0s 2ms/step - loss: 11.8243 Epoch 10/13 4/4 [==============================] - 0s 2ms/step - loss: 11.1492 Epoch 11/13 4/4 [==============================] - 0s 2ms/step - loss: 10.4892 Epoch 12/13 4/4 [==============================] - 0s 2ms/step - loss: 9.8249 Epoch 13/13 4/4 [==============================] - 0s 2ms/step - loss: 9.0948 2/2 [==============================] - 0s 2ms/step
mse = 8.024392817825545
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 1.048651 | 3.544737 | 2.496086 | 70.268226 |
| std | 11.113055 | 0.575967 | 1.911374 | 1.357362 | 3.610582 |
| min | 0.000000 | 0.349918 | 1.100000 | 0.750082 | 62.309921 |
| 25% | 9.250000 | 0.423397 | 1.425000 | 0.994972 | 67.671770 |
| 50% | 18.500000 | 1.166187 | 4.050000 | 2.954499 | 69.757323 |
| 75% | 27.750000 | 1.554964 | 5.075000 | 3.632096 | 73.297980 |
| max | 37.000000 | 1.908396 | 6.700000 | 4.862290 | 77.715922 |
con el cual obtenemos malos resultados.
Ahora, en vez de utilizar la función de activación ReLu utilizaremos la siguiente variante:
$$ LeakyReLU(x)=\left\{\begin{array}{c}x, x>0\\ \ 0, mx<0\end{array}\right. $$donde ésta en vez de enviar valores negativos a cero utiliza un parámetro de pendiente muy pequeño que incorpora cierta información de valores negativos. El problema que tenía nuestra red neuronal era justamente ese, en el cual los valores negativos se estaban yendo todos a cero, problema el cual queda solucionado con la función de activación ReLU con fugas (o 𝐿𝑒𝑎𝑘𝑦𝑅𝑒𝐿𝑈). Un detalle importante por mencionar es que con la función de activación ReLu la convergencia es más rápida, no obstante, para la ReLu con fugas dicha convergencia será un poco más lenta, de modo que implementaremos un mayor número de épocas.
De tal manera escribiremos
modelo2, df2, df_stats2 = modelo(40, 25, 'LeakyReLU', 50, False)
df_stats2
2/2 [==============================] - 0s 2ms/step
mse = 0.19440326062005897
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.489606 | 3.544737 | 0.355140 | 11.158327 |
| std | 11.113055 | 1.794334 | 1.911374 | 0.264809 | 6.957903 |
| min | 0.000000 | 1.318692 | 1.100000 | 0.007195 | 0.218022 |
| 25% | 9.250000 | 1.539637 | 1.425000 | 0.139637 | 5.891013 |
| 50% | 18.500000 | 3.859528 | 4.050000 | 0.275254 | 9.974061 |
| 75% | 27.750000 | 5.068981 | 5.075000 | 0.504230 | 14.585636 |
| max | 37.000000 | 6.162619 | 6.700000 | 1.062619 | 32.101742 |
con lo cual obtenemos mejores resultados, en realidad, dichos resultados son muy similares a los obtenidos con el modelo de regresión.
Recordemos que la función ReLu con fugas tiene un parámetro $m$ referente a la pendiente. Para modificar dicho valor podemos recurrir a tensorflow:
import tensorflow as tf
# ReLu con fugas configurando el valor de la pendiente m (alpha)
fun_activacion = lambda x: tf.keras.layers.LeakyReLU(alpha=x)
# alpha=0.3
modelo3, df3, df_stats3 = modelo(40, 25, fun_activacion(0.3), 50, False)
df_stats3
2/2 [==============================] - 0s 3ms/step
mse = 0.19706047023275194
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.454379 | 3.544737 | 0.348974 | 9.870676 |
| std | 11.113055 | 1.880185 | 1.911374 | 0.278051 | 6.661151 |
| min | 0.000000 | 1.181068 | 1.100000 | 0.012454 | 0.889572 |
| 25% | 9.250000 | 1.412454 | 1.425000 | 0.150619 | 4.534514 |
| 50% | 18.500000 | 3.837573 | 4.050000 | 0.285695 | 9.947510 |
| 75% | 27.750000 | 5.107232 | 5.075000 | 0.509004 | 13.324466 |
| max | 37.000000 | 6.261467 | 6.700000 | 1.161467 | 25.660315 |
notamos que con dicho valor hemos mejorado el modelo en cuanto al error promedio, el valor del cuartil al 75% y el valor máximo del error ha disminuido, en comparativa con el modelo de regresión. Así, hemos obtenido un mejor modelo con la red neuronal.
Continuamos en la búsqueda por el mejor modelo
# alpha=0.4
modelo4, df4, df_stats4 = modelo(40, 25, fun_activacion(0.4), 50, False)
df_stats4
2/2 [==============================] - 0s 3ms/step
mse = 0.19659494009660292
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.451361 | 3.544737 | 0.347851 | 9.836075 |
| std | 11.113055 | 1.877487 | 1.911374 | 0.278636 | 6.686215 |
| min | 0.000000 | 1.179924 | 1.100000 | 0.011312 | 0.807965 |
| 25% | 9.250000 | 1.411312 | 1.425000 | 0.147839 | 4.419739 |
| 50% | 18.500000 | 3.838183 | 4.050000 | 0.285953 | 10.035467 |
| 75% | 27.750000 | 5.102206 | 5.075000 | 0.509759 | 13.378070 |
| max | 37.000000 | 6.250940 | 6.700000 | 1.150940 | 25.720447 |
# alpha=0.7
modelo5, df5, df_stats5 = modelo(40, 25, fun_activacion(0.7), 50, False)
df_stats5
2/2 [==============================] - 0s 3ms/step
mse = 0.19503224669142566
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.486083 | 3.544737 | 0.355092 | 11.103247 |
| std | 11.113055 | 1.796349 | 1.911374 | 0.266092 | 6.860370 |
| min | 0.000000 | 1.314304 | 1.100000 | 0.002903 | 0.087982 |
| 25% | 9.250000 | 1.534458 | 1.425000 | 0.134458 | 6.131354 |
| 50% | 18.500000 | 3.855724 | 4.050000 | 0.270635 | 9.800012 |
| 75% | 27.750000 | 5.065818 | 5.075000 | 0.509000 | 14.651458 |
| max | 37.000000 | 6.164742 | 6.700000 | 1.064742 | 31.696852 |
Al aumentar el valor de alpha en 0.7 tenemos un peor rendimiento comparado con el modelo donde alpha=0.4.
# alpha=0.4
modelo6, df6, df_stats6 = modelo(40, 25, fun_activacion(0.4), 70, False)
df_stats6
2/2 [==============================] - 0s 3ms/step
mse = 0.1948398463071247
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.465775 | 3.544737 | 0.351841 | 10.496029 |
| std | 11.113055 | 1.832457 | 1.911374 | 0.270126 | 6.207114 |
| min | 0.000000 | 1.249901 | 1.100000 | 0.021658 | 0.656296 |
| 25% | 9.250000 | 1.474990 | 1.425000 | 0.146613 | 5.356446 |
| 50% | 18.500000 | 3.841792 | 4.050000 | 0.263687 | 10.423440 |
| 75% | 27.750000 | 5.077075 | 5.075000 | 0.514457 | 13.460788 |
| max | 37.000000 | 6.199116 | 6.700000 | 1.099116 | 28.404196 |
Tampoco parece ser lo correcto aumentar el número de épocas.
# alpha=0.4
modelo7, df7, df_stats7 = modelo(30, 20, fun_activacion(0.4), 70, False)
df_stats7
2/2 [==============================] - 0s 3ms/step
mse = 0.19387595750027908
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.467559 | 3.544737 | 0.350933 | 10.381939 |
| std | 11.113055 | 1.843523 | 1.911374 | 0.269506 | 6.190502 |
| min | 0.000000 | 1.239383 | 1.100000 | 0.019914 | 0.603461 |
| 25% | 9.250000 | 1.464303 | 1.425000 | 0.139465 | 4.651673 |
| 50% | 18.500000 | 3.847175 | 4.050000 | 0.275724 | 10.286566 |
| 75% | 27.750000 | 5.088551 | 5.075000 | 0.507647 | 13.014203 |
| max | 37.000000 | 6.216816 | 6.700000 | 1.116816 | 27.876862 |
ni dismiuir el número de neuronas. Aunque en los modelos anterior no obtenemos como tal un mal modelo.
Obtamos entonces por quedarnos con el modelo 4:
df_stats4
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.451361 | 3.544737 | 0.347851 | 9.836075 |
| std | 11.113055 | 1.877487 | 1.911374 | 0.278636 | 6.686215 |
| min | 0.000000 | 1.179924 | 1.100000 | 0.011312 | 0.807965 |
| 25% | 9.250000 | 1.411312 | 1.425000 | 0.147839 | 4.419739 |
| 50% | 18.500000 | 3.838183 | 4.050000 | 0.285953 | 10.035467 |
| 75% | 27.750000 | 5.102206 | 5.075000 | 0.509759 | 13.378070 |
| max | 37.000000 | 6.250940 | 6.700000 | 1.150940 | 25.720447 |
Recordemos que tanto la regresión lineal simple como el modelo de la red neurona solo ocuparon una variable con variable regresora. Lo que haremos ahora será la implementación de más variables predictorias. Así, la regresión lineal simple pasará a ser ahora una regresión lineal múltiple.
Para el caso de la regresión lineal simple únicamente consideramos una variable predictoria (petal_width). Luego, lo que ahoremos ahora será considerar 3 variables predictorias: sepal_length, sepal_width, petal_length.
Dado que efectuaremos también una regresión lineal, tendremos que dicha regresión será múltiple. En este caso mantendremos a petal_length como la variable de respuesta y consideraremos al resto (menos la variable species) como variables predictorias.
# Variables predictorias
X = df.drop(['petal_length', 'species'], axis=1).values
# variable de respuesta
y = df['petal_length'].values.reshape(-1,1)
# division de los datos
X_train, X_test, y_train, y_test = train_test_split(X, y, # conjunto completo
test_size=0.25, # 25% para pruebas
random_state=123) # semilla aleatoria
# instanciamos
reg = LinearRegression()
# ajustamos sobre los datos de entrenamiento
reg.fit(X_train, y_train)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
LinearRegression()
De nuevo creamos un dataframe con los valores predichos y con los valores de y_test
# predicion
y_pred_regression = reg.predict(X_test)
# dataframe con la informacion
df_info = pd.DataFrame(y_pred_regression).rename(columns = {0: 'y_pred_reg'})
df_info['y_test'] = y_test
df_info = df_info.reset_index()
# calculamos las diferencias entre los valores reales y los predichos
df_info['diff'] = abs(df_info.y_pred_reg - df_info.y_test)
# calculamos el porcentaje de error para cada fila
df_info['error'] = (df_info['diff'] * 100) / df_info['y_test']
df_info.head()
| index | y_pred_reg | y_test | diff | error | |
|---|---|---|---|---|---|
| 0 | 0 | 4.910943 | 4.9 | 0.010943 | 0.223320 |
| 1 | 1 | 5.797656 | 5.5 | 0.297656 | 5.411921 |
| 2 | 2 | 5.776232 | 5.6 | 0.176232 | 3.147003 |
| 3 | 3 | 3.749124 | 4.1 | 0.350876 | 8.557963 |
| 4 | 4 | 1.092527 | 1.4 | 0.307473 | 21.962350 |
Vemos, en primera instancia, una mejora entorno a los valores de las primeras predicción. De manera más profunda veamos las estadísticas sobre la columna error
df_info.describe()
| index | y_pred_reg | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.513231 | 3.544737 | 0.261164 | 9.621598 |
| std | 11.113055 | 1.925357 | 1.911374 | 0.232472 | 9.685099 |
| min | 0.000000 | 1.054751 | 1.100000 | 0.005467 | 0.089624 |
| 25% | 9.250000 | 1.492094 | 1.425000 | 0.058166 | 2.747729 |
| 50% | 18.500000 | 3.802773 | 4.050000 | 0.190130 | 6.897631 |
| 75% | 27.750000 | 4.906221 | 5.075000 | 0.363613 | 13.271660 |
| max | 37.000000 | 6.763899 | 6.700000 | 0.989029 | 35.823164 |
Notamos que el error promedio es menor en comparativa con el modelo de regresión lineal simple, aunque la desviación estándar y el error máximo aumentaron para el caso de la regresión lineal múltiple.
Veamos algunas métricas:
# error cuadratico medio
mse = mean_squared_error(y_pred_regression, y_test)
# R^2
r2 = r2_score(y_pred_regression, y_test)
# veamos
print(f'mse = {mse}\nR^2 = {r2}')
mse = 0.12082769704546548 R^2 = 0.9665245914976561
donde tenemos que:
| métrica | reg lineal simple | reg lineal múltiple |
|---|---|---|
| $mse$ | 0.1949 | 0.1208 |
| $R^2$ | 0.938 | 0.9665 |
es decir, tenemos mejores resultados con el modelo de regresión lineal múltiple. Finalemnte veamos el gráfico de los datos reales versus los predichos
plt.plot(df_info.index, df_info.y_pred_reg, color='blue', label='prediccioón')
plt.plot(df_info.index, df_info.y_test, color='red', label='real')
plt.legend()
plt.grid()
plt.show()
en el cual sí notamos una mejora en el ajuste comparando dicha gráfica con la obtenida en la regresión lineal simple:
Realizaremos un pequeño cambia para input_shape en la siguiente función
def modelo(n1, n2, activacion, epocas, boolean):
"""
n1: número de neuronas en la primer capa
n2: número de neuronas en la segunda capa
activacion: función de activación en la última capa
epocas: número de épocas
boolean: booleano para determinar el valor de verbose
"""
# Instanciamos el modelo
model = Sequential()
# Capa de entrada de 1 neurona y capa oculta de n1 neuronas.
# Para la capa oculta utilizamos la funcion de activacion relu
model.add(Dense(n1, activation='relu', input_shape=(3,)))
# Capa oculta 2:
# n2 neuronas y funcion de activacion relu
model.add(Dense(n2, activation='relu'))
# Capa de salida con funcion de activacion "activacion"
model.add(Dense(1, activation=activacion))
# Compilacion. Utilizaremos ahora el error cuadratico medio
model.compile(optimizer='adam', loss='mean_squared_error')
# Entrenamiento
modelo = model.fit(X_train, y_train, epochs=epocas, verbose = boolean)
# prediccion
y_pred = model.predict(X_test)
# dataframe con la informacion
df = pd.DataFrame(y_pred).rename(columns = {0: 'y_pred'})
df['y_test'] = y_test
df = df.reset_index()
df['diff'] = abs(df.y_pred - df.y_test)
df['error'] = (df['diff'] * 100) / df['y_test']
# estadisticas
df_stats = df.describe()
# grafica
plt.plot(df.index, df.y_pred, color='blue', label='prediccioón')
plt.plot(df.index, df.y_test, color='red', label='real')
plt.legend()
plt.grid()
plt.show()
# MSE
mse = mean_squared_error(y_pred, y_test)
print(f'mse = {mse}')
return modelo, df, df_stats
pues recordemos que ahora estamos trabajando con 3 variables predictorias. Luego, implementamos los mismos valores configurados en el modelo 4
# Para este caso aumentamos el numero de epocas
modelo1_mult, df1_mult, df_stats1_mult = modelo(40, 25, fun_activacion(0.4), 70, False)
df_stats1_mult
2/2 [==============================] - 0s 3ms/step
mse = 0.11747747303302854
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.527997 | 3.544737 | 0.253141 | 8.675280 |
| std | 11.113055 | 1.903661 | 1.911374 | 0.234180 | 8.862192 |
| min | 0.000000 | 1.136449 | 1.100000 | 0.017433 | 0.355767 |
| 25% | 9.250000 | 1.475468 | 1.425000 | 0.051992 | 2.398264 |
| 50% | 18.500000 | 3.828365 | 4.050000 | 0.169351 | 6.640920 |
| 75% | 27.750000 | 4.959173 | 5.075000 | 0.377703 | 10.674295 |
| max | 37.000000 | 6.720815 | 6.700000 | 0.962185 | 33.820804 |
Notamos también una mejora respecto al resultado obtenido en el modelo 4 (en el cual solo trabajamos con una variable predictoria):
Podemos comparar estadísticas del modelo 4 con una variable predictoria, al modelo implementado antes con 3 variables predictorias
display(df_stats4)
print()
display(df_stats1_mult)
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.451361 | 3.544737 | 0.347851 | 9.836075 |
| std | 11.113055 | 1.877487 | 1.911374 | 0.278636 | 6.686215 |
| min | 0.000000 | 1.179924 | 1.100000 | 0.011312 | 0.807965 |
| 25% | 9.250000 | 1.411312 | 1.425000 | 0.147839 | 4.419739 |
| 50% | 18.500000 | 3.838183 | 4.050000 | 0.285953 | 10.035467 |
| 75% | 27.750000 | 5.102206 | 5.075000 | 0.509759 | 13.378070 |
| max | 37.000000 | 6.250940 | 6.700000 | 1.150940 | 25.720447 |
| index | y_pred | y_test | diff | error | |
|---|---|---|---|---|---|
| count | 38.000000 | 38.000000 | 38.000000 | 38.000000 | 38.000000 |
| mean | 18.500000 | 3.527997 | 3.544737 | 0.253141 | 8.675280 |
| std | 11.113055 | 1.903661 | 1.911374 | 0.234180 | 8.862192 |
| min | 0.000000 | 1.136449 | 1.100000 | 0.017433 | 0.355767 |
| 25% | 9.250000 | 1.475468 | 1.425000 | 0.051992 | 2.398264 |
| 50% | 18.500000 | 3.828365 | 4.050000 | 0.169351 | 6.640920 |
| 75% | 27.750000 | 4.959173 | 5.075000 | 0.377703 | 10.674295 |
| max | 37.000000 | 6.720815 | 6.700000 | 0.962185 | 33.820804 |
notamos mejoras en el modelo modelo1_mult, pero el modelo 4 mantiene un menor número referente a la desviacón estándar y al error máximo cometido. De tal manera vemos que cada modelo tendrá sus ventajas y desventajas.