Redes neuronales¶


Clase8: Redes neuronales¶


Autor: Luis Fernando Apáez Álvarez

Contenido¶

  • Capas densas
    •
  • Funciones de activación
    •
  • Optimizadores
    •

En esta clase nos centraremos en entrenar una red neuronal utilizando tensorflow. A lo largo de la clase trabajaremos con un conjunto de datos sobre incumplimiento de tarjetas de crédito, el cual contiene características como el estado civil y el monto de pago, información que utilizaremos para la predicción de determinado objetivo que tomará valores continuos. Por ejemplo, si tenemos que en estado civil es soltero, tendrá asociado un valor de 0 (caso contrario pondremos un valor de 1) y que el monto de pago es de 100, entonces mediante una ponderación, digamos por ejemplo

$$ 100(0.10) + 0(-0.25)=10 $$

tendremos un valor de predicción obtenido de 10, para cierto objetivo. El proceso anterior parecer ser una regresión lineal, lo cual ya se ha mencionado en clases anteriores.

Capa densa ¶

En esta clase trabajaremos con redes neuronales cuyas capas sean densas, donde una capa densa aplica pesos a todos los nodos de la capa anterior

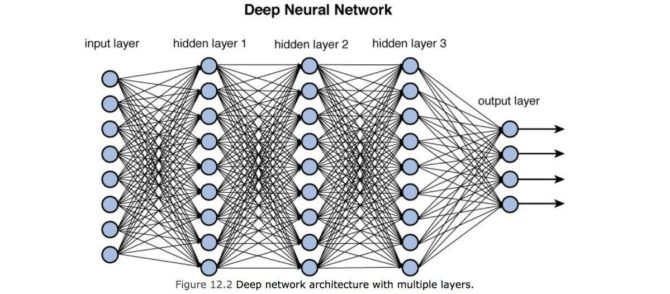
Veamos un ejemplo sencillo de una capa densa implementado en tensorflow:

  • Definimos las entradas (características) mediante un tensor constante, el cual contine la información del estado civil y la información de la edad
In [10]:
import tensorflow as tf
inputs = tf.constant([[1.0, 35.0]])
inputs
Out[10]:
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[ 1., 35.]], dtype=float32)>
  • Luego, inicializaremos los pesos como una variable, debido a que entrenaremos esos pesos para predecir la salida de las entradas. También, definiremos un sesgo (el cual juega un papel muy similar al intercepto en el modelo de regresión lineal)
In [7]:
weights = tf.Variable([[-0.05], [-0.01]])
bias = tf.Variable([0.5])
print(weights)
print(bias)

<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[-0.05],
       [-0.01]], dtype=float32)>
<tf.Variable 'Variable:0' shape=(1,) dtype=float32, numpy=array([0.5], dtype=float32)>
  • Finalmente definimos una capa densa. Debemos tener en cuenta que primero realizaremos una multiplicación matricial de las entradas por los pesos
In [11]:
product = tf.matmul(inputs, weights)
product
Out[11]:
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[-0.4]], dtype=float32)>
  • Agregamos dicho producto al sesgo (product + bias), y lo que haremos será aplicar una transformación no lineal como función de activación, en este caso la función sigmoide:
In [14]:
print(product + bias)
print()

dense = tf.keras.activations.sigmoid(product + bias)
print(dense)

tf.Tensor([[0.09999999]], shape=(1, 1), dtype=float32)

tf.Tensor([[0.5249792]], shape=(1, 1), dtype=float32)

Básicamente, con lo anterior tenemos gráficamente:

re1.PNG

De tal manera, el código completo de la capa densa simple definida antes es:

In [16]:
# Informacion de entrada
inputs = tf.constant([[1.0, 35.0]])

# Pesos iniciales
weights = tf.Variable([[-0.05], [-0.01]])
bias = tf.Variable([0.5])

# Producto matricial entre las entradas y los pesos
product = tf.matmul(inputs, weights)

# Definicion de la capa densa con funcion de activacion
# sigmoidea
dense = tf.keras.activations.sigmoid(product + bias)
dense
Out[16]:
<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.5249792]], dtype=float32)>

Tensorflow cuenta con operaciones de alto nivel, como tf.keras que permite saltarnos el álgebra lineal. Por ejemplo

# Definimos la informacion de entrada
inputs = tf.constant(data, tf.float32)

# Definimos la primera capa densa oculta.
dense1 = tf.keras.layers.Dense(10, activation='sigmoid')(inputs)

El primer argumento específica el número de nodos salientes, en el ejemplo anterior hemos específicado 10 nodos salientes, y el segundo argumento es la función de activación a utilizar. De forma predeterminada se incluirá el sesgo. Además, notamos que se han pasado las entradas como argumento para la primera capa densa.

Definamos otra capa densa

# Definimos la segunda capa densa oculta.
# Ahora con 5 nodos de salida
dense2 = tf.keras.layers.Dense(5, activation='sigmoid')(dense1)

donde ahora pasamos como argumento a la segunda capa densa, la información de la primer capa densa. Finalmente definimos la capa de salida

# Capa de salida
outputs = tf.keras.layers.Dense(1, activation='sigmoid')(dense2)

donde se pasa como argumento la información obtenida de la capa densa 2, y tendremos un nodo de salida.

re2.PNG

Podemos mencionar algunas comparaciones entre los enfoques de alto y bajo nivel:

alto bajo
Se basan en operaciones complejas de alto nivel (como Keras) lo cual reduce la cantidad de código Utiliza álgebra lineal, lo cual permite la construcción de cualquier modelo

Tensorflow permite trabajar con ambos enfoques, incluso permite combinarlos.

Por otro lado, veamos un esquema de código en el cual podemos definir una red neuronal con dos capas ocultas:

# Informacion de entrada
inputs = tf.constant(data, tf.float32)

# Pesos iniciales y bias referentes a la primer capa oculta
weights1 = tf.Variable(ones((3,2)))
bias1 = tf.Variable(1.0)
# Producto matricial entre las entradas y los pesos
product1 = tf.matmul(inputs, weights1)
# Definicion de la capa densa1 con funcion de activacion
# sigmoidea
dense1 = tf.keras.activations.sigmoid(product1 + bias1)

# Mutiplicamos la informacion de la capa 1 con los segundos pesos
weights2 = tf.Variable(ones((2,1)))
bias2 = tf.Variable(1.0)
product2 = tf.matmul(dense1, weights2)

# Finalmente tenemos la capa de salida
outputs = tf.keras.activations.sigmoid(product2 + bias2)

donde siempre debe tenerse cuidado con las formas (shape) de los distintos componentes de la red neuronal para aplicar de manera correcta la multiplicación matricial.

Funciones de activación ¶

Una capa oculta típica consiste de dos operaciones. El primero realiza la multiplicación de matrices, lo cual es una operación lineal y el segundo aplica una funcón de activación, lo cual es una operación no lineal.

Veamos un ejemplo simple, donde asumimos que el peso sobre la edad es 1 y el peso sobre el monto de la factura es de 2

In [5]:
import numpy as np
import tensorflow as tf

# Proporcion de edad, esto es, edad / 1000
joven, viejo = 0.3, 0.6

# Proporcion del monto de las facturas, 
# esto es, monto  / 10000
factura_baja, factura_alta = 0.1, 0.5

# Aplicamos el paso de multiplicacion matricial para todas las
# posibles combinaciones de las caracteristicas
joven_alta = 1.0 * joven + 2.0 * factura_alta
joven_baja = 1.0 * joven + 2.0 * factura_baja
viejo_alta = 1.0 * viejo + 2.0 * factura_alta
viejo_baja = 1.0 * viejo + 2.0 * factura_baja

Si no aplicamos la función de activación y asumimos que el sesgo es cero, encontraremos que el impacto del monto de la factura no depende de la edad

In [6]:
print(joven_alta - joven_baja)
print(viejo_alta - viejo_baja)

0.8
0.8

donde en ambos casos predecimos un valor de 0.8.

Tenemos entonces un error pues, el monto de factura sí depende de la edad. Veamos ahora lo que ocurre si aplicamos una transformación no lineal, por ejemplo la función sigmoidea

In [7]:
print(tf.keras.activations.sigmoid(joven_alta)-tf.keras.activations.sigmoid(joven_baja))
print(tf.keras.activations.sigmoid(viejo_alta)-tf.keras.activations.sigmoid(viejo_baja))

tf.Tensor(0.16337568, shape=(), dtype=float32)
tf.Tensor(0.14204389, shape=(), dtype=float32)

con lo cual obtentemos resultados distintos.

Dentro de las funciones de activación tendremos algunas populares como:

  • Sigmoide: Se utiliza principalmente en la capa de salida de los problemas de clasificación binaria.
  • relu: Por lo general se utilizará en todas las capas que no sean la capa de salida

  • Softmax: Se utiliza en la capa de salida en problemas de clasificación con más de dos clases. Las salidas de una función de activación softmax se pueden interpretar como probabilidades de clase en problemas de clasificación multiclase. Por ejemplo, si consideramos las siguientes probabilidades en la capa de salida:
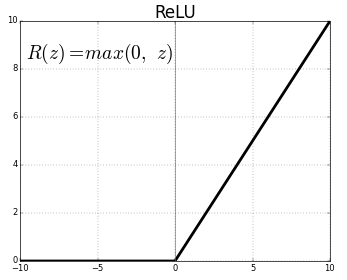
0.4 --> clase1
0.9 --> clase2
0.1 --> clase3

tendremos entonces que la salida es más probable que pertenezca a la clase 2.

Veamos un ejemplo de red neuronal, para un determinado problema de clasificación multiclase, implementando las funciones de activación:

# Alto nivel:

# Entrada
inputs = tf.constant(features, tf.float32)

# Capa densa 1
dense1 = tf.keras.layers.Dense(16, activation = 'relu')(inputs)

# Capa densa 2
dense2 = tf.keras.layers.Dense(8, activation = 'sigmoid')(dense1)

# Salida
outputs = tf.keras.layers.Dense(4, activation = 'softmax')(dense2)

Optimizadores ¶

En el entrenamiento de una red neuronal inicializamos de manera aletoria los pesos, punto de partida, después medimos la pérdida y luego intentamos pasar a obtener una pérdida menor, esto es, deseamos minimizar la función de pérdida de acuerdo al ajuste de los pesos. Para llevar a cabo este proceso utilizaremos el algoritmo del descenso del gradiente. En particular sabemos que el descenso del gradiente tiene peligro en quedars estancado en un mínimo local. Para resolver dicho problema utilizamos el descenso del gradiente estocástico.

Veremos un ejemplo en tensorflow para algunos optimizadores, de donde:

  • Optimizador SGD (descenso estocástico del gradiente): Lo utilizaremos mediante tf.keras.optimizers.SGD(), requerimos de una valor para la tasa de aprendizaje (determina qué tan rápido se ajustan los parámetros del modelo).

  • Optimizador RMS (optimizador de propagación): Aplica diferentes tasas de aprendizaje a cada función (lo cual es sutil para problemas de alta dimensión). Además tiene dos parámetros momentum y decay (al establecer un valor bajo para este parámetro evitará que el momentum se acumule durante largos períodos durante el entrenamiento). tf.keras.optimizers.RMSprop()

  • Optimizador ADAM: tf.keras.optimizers.Adam(), optimizador adaptativo. Proporciona mejoras adicionales y generalmente es una buena primera opción de elección. Es similar a RMS al configurar el momentum para que decaiga más rápido al reducir el parámetro beta1.

Veamos un ejemplo. Supongamos que las características y los pesos se han inicializado, referentes al problema sobre el crédito bancario con el cual hemos estado trabajando. Luego, definiremos un modelo que calcula las predicciones y una función de activación sigmoidea

import tensorflow as tf

# Definimos una funcion del modelo
def model(bias, weigths, features=b_features):
    product = tf.matmul(features, weigths)
    return tf.keras.activations.sigmoid(product + bias)

Luego, definimos la función de pérdida mediante binary_crossentropy, la cual es el estándar para los problemas de clasificación binaria

# Calculamos los valores predictivos y la perdida
def loss_function(bias, weigths, targets=default, features=b_features):
    predictions = model(bias, weigths)
    return tf.keras.losses.binary_crossentropy(target, predictions)

Finalmente, definimos un optimizador utilizando RMS

# definicion del optimizador
op = tf.keras.optimizaer.RMSprop(learning_rate=0.01, momentum=0.9)
# minimizacion de la funcion de perdida, donde dicha funcion
# es de dos variables: bias y weights
opt.minimize(lambda: loss_function(bias, weights), var_list=[bias, weights])

Por otro lado, intentemos hallar el mínimo global de una función mediante el optimizador SGD

rrs1.PNG

donde vemos que podemos caer en el mínimo local que se ve en el punto rojo de la izquierda. Para ello considereraremos

import tensorflow as tf

# Inicializamos dos variables
x1 = tf.Variable(5.0, tf.float32)
x2 = tf.Variable(0.5, tf.float32)

# Definimos el optimizador
opt = tf.keras.optimizers.SGD(learning_rate=0.01)

# Realizaremos el proceso de minimizacion 100 veces
for j in range(100):
    # Suponiendo que loss_function() corresponde a la funcion
    # cuya grafica es la que vimos en la imagen, configuramos
    # la minimizacion usando dicha funcion para x1
    opt.minimize(lambda: loss_function(x1), var_list=[x1])
    # lo mismo para x2
    opt.minimize(lambda: loss_function(x2), var_list=[x2])
# Imprimimos los valores resultantes
print(x1.numpy(), x2.numpy())

lo cual nos arrojaría 4.38 0.42.

Notamos que para x1 el valor se acercó al mínimo global, y para x2 al mínimo local, lo cual es por cómo inicializamos los valores de las variables. Tenemos entonces que x2 se ha estancado en el mínimo local.

Veamos ahora lo que obtenemos al cambiar el momentum:

# Inicializamos dos variables
x1 = tf.Variable(0.05, tf.float32)
x2 = tf.Variable(0.05, tf.float32)

# Definimos el optimizador
opt1 = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.99)
opt2 = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.00)

# Realizaremos el proceso de minimizacion 100 veces
for j in range(100):
    # Suponiendo que loss_function() corresponde a la funcion
    # cuya grafica es la que vimos en la imagen, configuramos
    # la minimizacion usando dicha funcion para x1
    opt1.minimize(lambda: loss_function(x1), var_list=[x1])
    # lo mismo para x2
    opt2.minimize(lambda: loss_function(x2), var_list=[x2])
# Imprimimos los valores resultantes
print(x1.numpy(), x2.numpy())

donde se obtendría 4.31 0.42, lo que nos dice que x1 a pesar de su valor inicial no se ha estancado en el mínimo local debido al momentum que se ha definido. En cambio, x2 sí se ha estancado debido a que hemos establecido un valor del momentum de cero.

Finalmente:

In [5]:
# Un ejemplo de minimizacion 
import tensorflow as tf

# Funcion a minimizar
def f(x):
    return x ** 2

# Inicializamos dos variables
x1 = tf.Variable(5.0, tf.float32)
x2 = tf.Variable(0.5, tf.float32)

# Definimos el optimizador
opt = tf.keras.optimizers.SGD(learning_rate=0.01)

# Realizaremos el proceso de minimizacion 100 veces
for j in range(100):
    # Suponiendo que loss_function() corresponde a la funcion
    # cuya grafica es la que vimos en la imagen, configuramos
    # la minimizacion usando dicha funcion para x1
    opt.minimize(lambda: f(x1), var_list=[x1])
    # lo mismo para x2
    opt.minimize(lambda: f(x2), var_list=[x2])
# Imprimimos los valores resultantes
print(x1.numpy(), x2.numpy())

0.66309786 0.06630978

notamos que en ambos casos los valores se van aproximando a 0, pero para x2 la aproximación es mejor pues su valor inicial fue más cercano a cero. Repetimos pero ahora realizando más iteraciones.

In [6]:
# Realizaremos el proceso de minimizacion 1000 veces
for j in range(1000):
    # Suponiendo que loss_function() corresponde a la funcion
    # cuya grafica es la que vimos en la imagen, configuramos
    # la minimizacion usando dicha funcion para x1
    opt.minimize(lambda: f(x1), var_list=[x1])
    # lo mismo para x2
    opt.minimize(lambda: f(x2), var_list=[x2])
# Imprimimos los valores resultantes
print(x1.numpy(), x2.numpy())

1.1159718e-09 1.11597134e-10

Ahora en ambos casos nos hemos acercado mejor al cero.

Veamos ahora lo que ocurre si cambiamos el momentum

In [8]:
# Inicializamos dos variables
x1 = tf.Variable(5.0, tf.float32)
x2 = tf.Variable(0.5, tf.float32)

# iremos variando el momentum
for m in [0.1 * i for i in range(10)]:
    # Definimos el optimizador
    opt = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=m)

    # Realizaremos el proceso de minimizacion 100 veces
    for j in range(100):
        # Suponiendo que loss_function() corresponde a la funcion
        # cuya grafica es la que vimos en la imagen, configuramos
        # la minimizacion usando dicha funcion para x1
        opt.minimize(lambda: f(x1), var_list=[x1])
        # lo mismo para x2
        opt.minimize(lambda: f(x2), var_list=[x2])
    # Imprimimos los valores resultantes
    print(f'{x1.numpy()}, {x2.numpy()}. Momentum={m}')

0.6630978584289551, 0.06630977988243103. Momentum=0.0
0.06985821574926376, 0.006985819432884455. Momentum=0.1
0.005499826744198799, 0.0005499824183061719. Momentum=0.2
0.0002956187818199396, 2.956185198854655e-05. Momentum=0.30000000000000004
9.402451723872218e-06, 9.402444902661955e-07. Momentum=0.4
1.3768524809165683e-07, 1.3768520545909269e-08. Momentum=0.5
5.48607326233963e-10, 5.486071319449337e-11. Momentum=0.6000000000000001
1.0725769502163002e-13, 1.0725768993943233e-14. Momentum=0.7000000000000001
-2.1038466204740015e-18, -2.1038471633112785e-19. Momentum=0.8
-8.895295935622822e-21, -8.895295531726039e-22. Momentum=0.9

notamos que el momentum=0.4, la aproximación para ambos casos es muy buena, y a partir de ahí las aproximaciones mejoran en ambos casos.