Autor: Luis Fernando Apáez Álvarez
El algoritmo del descenso del gradiente es uno de los algoritmos de optimización más populares, especialmente en el campo de las redes neuronales. Descenso del gradiente es un método general para la minimización de cualquier función $f$, así como vimos una pequeña prueba al final de la clase pasada.
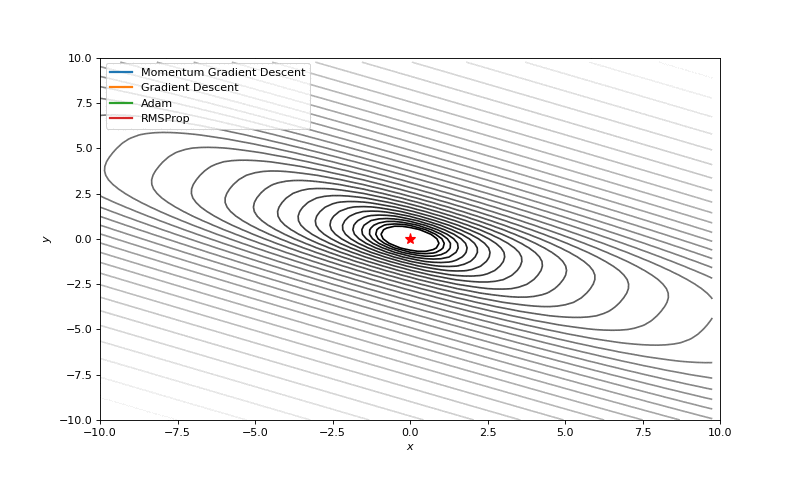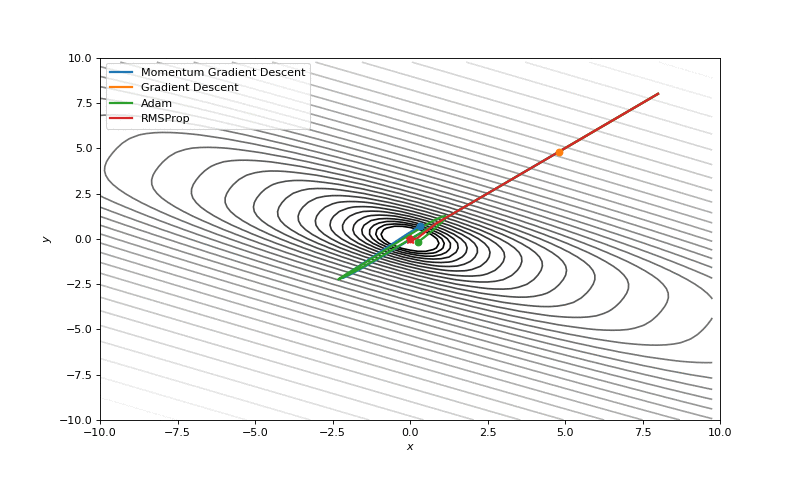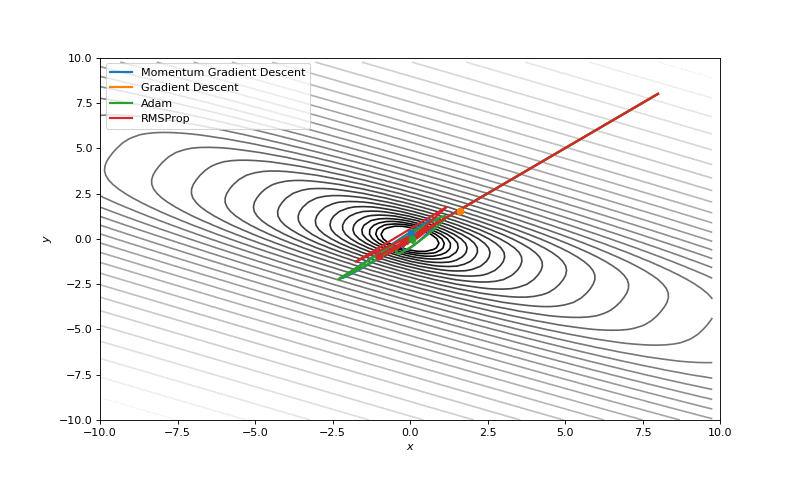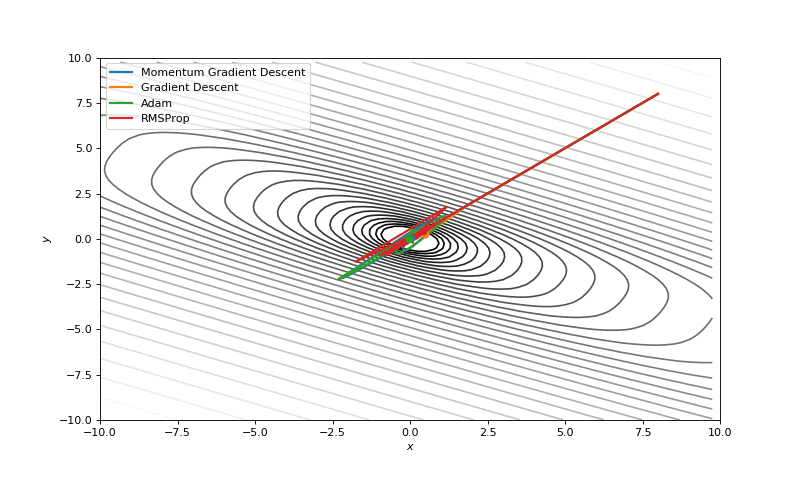
Básicamente el algoritmo toma la derivada de la función en cuestión, pues ésta mide la rapidez con que cambia la función, esto es, cuando crece o decrece. Calculando la pendiente en un punto en específico, sabremos en ese punto cuando la función crece, de modo que podemos seguir la dirección contraria a la pendiente obtenida e iremos bajando hasta un punto mínimo.
EL gradiente de una función $f$ es la generalización vectorial de la derivada, siendo éste un vector que contiene la información de cuando crece la función en un punto en específico $x=(x_{1},\ldots,x_{n})$, donde:
$$ \nabla f=\left[\frac{\partial f}{\partial x_{1}},\ldots, \frac{\partial f}{\partial x_{n}}\right] $$Ahora bien, el tamaño de paso con el cual vamos avanzando rumbo al mínimo de la función se conoce como tasa de aprendizaje. Un critero del paso puede ser que, cuando la función crece mucho, entonces debemos de descender mucho también; si crece poco, entonces sería conveniente también ir descendiendo poco. Esto es, el paso es proporcional al gradiente. Para poder controlar la proporción del paso utilizaremos un parámetro adicional $k$, de modo que el paso a dar se cuantifica como: $-k\nabla$.
Así, dada una posición inicial en el punto $x$, podemos avanzar a una nueva posición $\hat{x}$ que dependerá del paso que demos, del tamaño y de la dirección:
$$ \hat{x}=x-k\nabla f(x) $$Para cada nueva posición podemos medir $\hat{x}-x$, y si esta cantidad es menor que cierto umbral o si alcanzamos cierto número de iteraciones, podemos decir, prácticamente, que hemos alcanzado el mínimo de la función.
La siguiente imagen representa el recorrido iterativo de las nuevas posiciones:
Cabe mencionar que este algoritmo no garantiza que lleguemos al punto mínimo, pues puede ocurrir que éste nos conduzca a un mínimo local de uan función.
Para resolver dicho problema podemos implementar adaptatibilidad a la tasa de aprendizaje $k$, esto es, ir cambiando el valor de $k$ con el tiempo. La idea anterior básicamente nos ayudará a que la búsqueda no se estabilice en un mínimo local, pues si aumentamos el valor de $k$ podemos saltar posibles caminos que nos conduzcan a los mínimos locales
conduciéndonos así al mínimo global. La modificación de la $k$ a lo largo del tiempo puede ser implementada mediante una recta, o de alguna otra forma como un comportamiento logarítmico entre otros. Para ello consideramos el par $(t_{i}, k_{i})$ que hace referencia al valor de la tasa de aprendizaje $k_{i}$ en el tiempo $t_{i}$. Por ejemplo, si consideramos $i=1,\ldots,n$, entonces la ecuación de la recta que describe el comportamiento está dada por:
$$ m = \frac{k_{n}-k_{0}}{t_{n}-t_{0}} \ \ \ \Rightarrow \ \ k(t)=mt+k_{0} $$Con lo cual el valor de la tasa de aprendizaje cambiará en el tiempo, permitiéndonos así que el algoritmo del descenso del gradiente no se estabilice en un mínimo local.
Recordemos que la inicialización de los pesos en una red neuronal es de manera aleatoria. A partir de ello se procederá de manera iterativa siguiendo un algoritmo de optimización, dentro del cual se tratará de minimizar las diferencias entre la salida real y la estimada por la red neuronal. Para ello, es común que sea empleado el algoritmo del descenso del gradiente para ajustar los parámetros de la red para minimizar los errores.
El algoritmo del descenso del gradiente utilizado para el entrenamiento de una red sigue los siguientes pasos:
Estaremos repitiendo los pasos anteriores mientras el valor de la función de coste y las métricas de salida no empiecen a empeorar de manera sostenida.
Por otro lado, podemos conocer cómo varía el gradiente realizando el cálculo de las segundas derivadas, no obstante, este proceso representa un costo computacional elevado. Para ello existe diversas técnicas de aproximación donde se estiman las segundas derivadas, algunas de ellas son:
